- Runzhong Wang, Shanghai Jiao Tong University, China
- Junchi Yan (corresponding author), Shanghai Jiao Tong University, China
- Xiaokang Yang, Shanghai Jiao Tong University, China
This project page includes the dataset of our PAMI paper on unsupervised learning of deep graph matching models, covering two-graph matching, multi-graph matching and matching with a mixture of modes.
Abstract
Graph matching (GM) has been a long-standing combinatorial problem due to its NP-hard nature. Recently (deep) learning-based approaches have shown their superiority over the traditional solvers while the methods are almost based on supervised learning which can be expensive or even impractical. We develop a unified unsupervised framework from matching two graphs to multiple graphs, without correspondence ground truth for training. Specifically, a Siamese-style unsupervised learning framework is devised and trained by minimizing the discrepancy of a second-order classic solver and a first-order (differentiable) Sinkhorn net as two branches for matching prediction. The two branches share the same CNN backbone for visual graph matching. Our framework further allows unsupervised learning with graphs from a mixture of modes which is ubiquitous in reality. Specifically, we develop and unify the graduated assignment (GA) strategy for matching two-graph, multi-graph, and graphs from a mixture of modes, whereby two-way constraint and clustering confidence (for mixture case) are modulated by two separate annealing parameters, respectively. Moreover, for partial and outlier matching, an adaptive reweighting technique is developed to suppress the overmatching issue. Experimental results on real-world benchmarks including natural image matching show our unsupervised method performs comparatively and even better against two-graph based supervised approaches.
- Two Graph Matching (2GM): Matching two graphs from the same category;
- Multi-Graph Matching (MGM): Joint matching of more than two graphs from the same category;
- Multi-Graph Matching with a Mixture of Modes (MGM3): Joint matching of more than two graphs from different categories.
Specifically, this paper considers the settings of partial & outlier matching and matching of a mixture of modes:
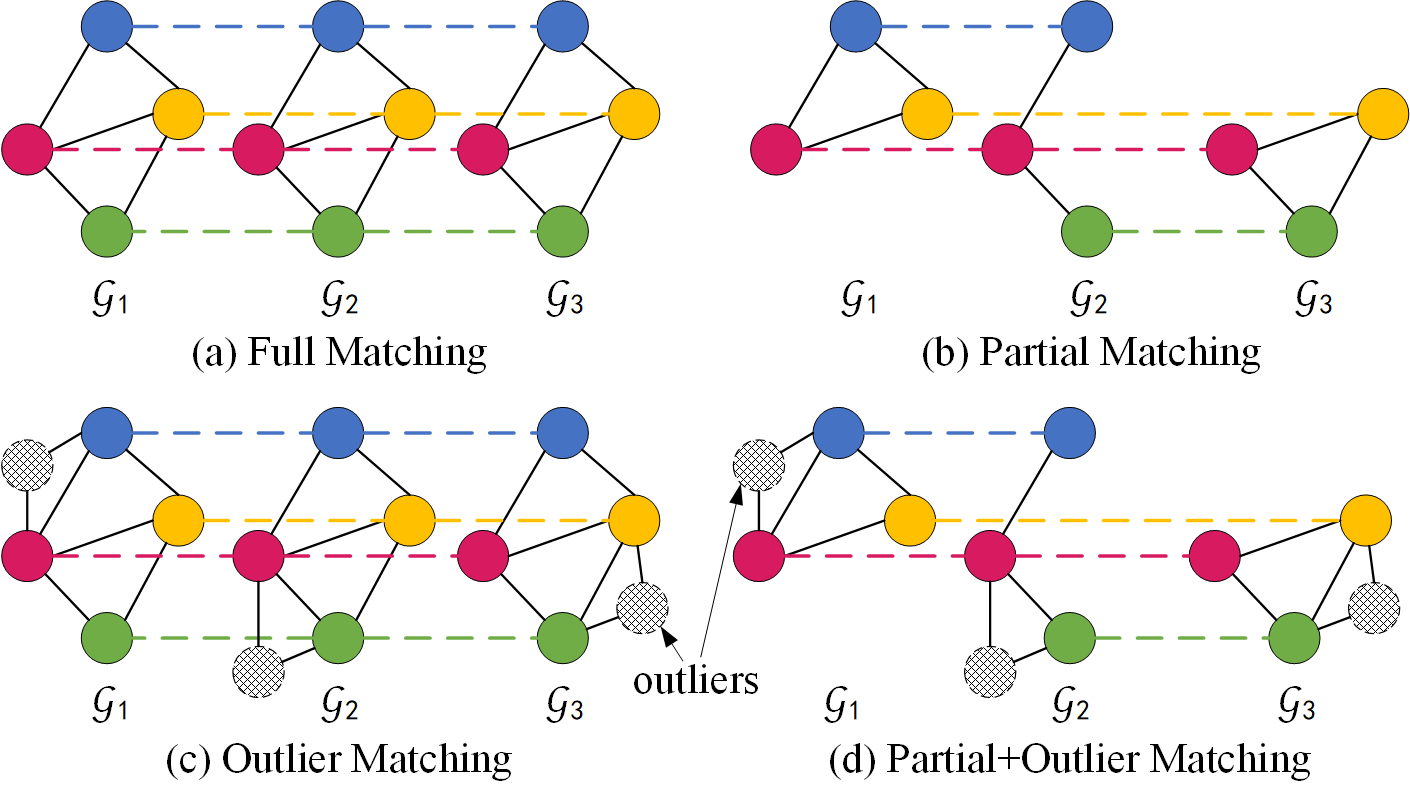
Figure 1. Comparison of the four GM settings over multiple graphs (same color denotes correspondence): (a) the classical full matching where all node pairs have a valid matching, (b) partial matching where some inlier nodes are occluded and all nodes partially correspond to a universe (here the universe has 4 nodes), (c) outlier matching where the noisy outliers do not correspond to any nodes in the universe, (d) the mix of both partial and outlier matching, which is the most challenge yet the most realistic setting. Most existing papers only consider (a), some recent efforts also consider (b), and in this paper we propose a robust approach considering (a)(b)(d). (c) is less common because outliers usually appear together with partial matching.
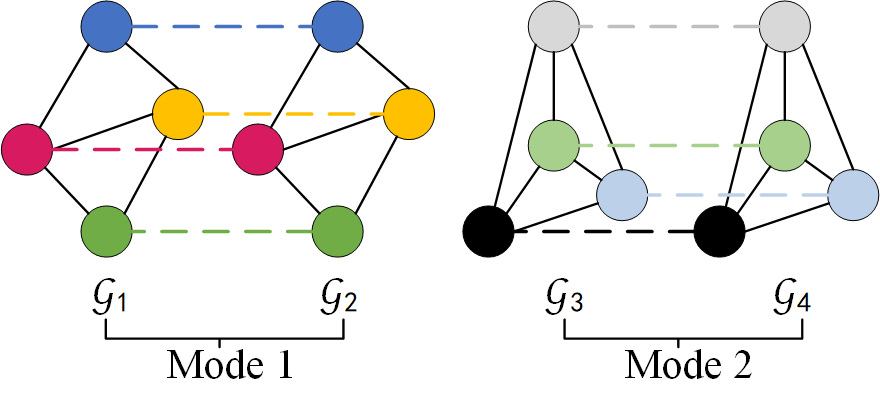
Figure 2. Example of matching with a mixture of two modes. Within mode 1 or mode 2 (intra-mode) there is full-matching, and between mode 1 and mode 2 (inter-mode) the matching is non-valid.
Our proposed unsupervised learning framework is a discrepancy-minimization framework: The learning target is to minimize the discrepancy between a Sinkhorn branch and a GM solver branch.
The Sinkhorn branch is differentiable, and the GM solver branch naturally truncates the gradient, prohibiting the Siamese framework from degenerating to trivial solutions.
Here the GM solver in white box can be any of solvers for matching either of two-graph, multi-graph, or graphs from a mixture of modes. CNN features are learned in this unsupervised learning framework.

Figure 3. The red modules support gradient back-propagation, and the white modules do not.
To fulfill the unified framework for all graph matching settings, we resort to the classic graduated assignment (GA) algorithm as the embodiment of GM solver. Specifically, we combine the classic GA algorithm with modern deep learning models, and we propose three unsupervised graduated assignment models:
- GANN-2GM for two graph matching (2GM);
- GANN-MGM for multi-graph matching (MGM);
- GANN-MGM3 for multi-graph matching with a mixture of modes (MGM3).
A brief summary of results:
The performance of unsupervised models are comparative or even better than state-of-the-art supervised graph matching models.
Experiment Results on Willow Object Class dataset (2GM and MGM): unsupervised models are as strong as supervised models.
| method | learning | car | duck | face | mbike | wbottle | mean |
|---|---|---|---|---|---|---|---|
| Learning-free Solvers | |||||||
| MatchLift (Chen et al. ICML 2014) | free | 0.665 | 0.554 | 0.931 | 0.296 | 0.700 | 0.629 |
| MatchALS (Zhou et al. ICCV 2015) | free | 0.629 | 0.525 | 0.934 | 0.310 | 0.669 | 0.613 |
| MSIM (Wang et al. CVPR 2018) | free | 0.750 | 0.732 | 0.937 | 0.653 | 0.814 | 0.777 |
| MGM-Floyd (Jiang et al. PAMI 2020) | free | 0.850 | 0.793 | 1.000 | 0.843 | 0.931 | 0.883 |
| HiPPI (Bernard et al. ICCV 2019) | free | 0.740 | 0.880 | 1.000 | 0.840 | 0.950 | 0.882 |
| VGG16+Sinkhorn | free | 0.776±0.238 | 0.732±0.253 | 0.990±0.044 | 0.525±0.205 | 0.824±0.190 | 0.769 |
| GA-GM (ours) | free | 0.814±0.300 | 0.885±0.197 | 1.000±0.000 | 0.809±0.243 | 0.954±0.113 | 0.892 |
| GA-MGM (ours) | free | 0.746±0.153 | 0.900±0.106 | 0.997±0.021 | 0.892±0.139 | 0.937±0.072 | 0.894 |
| Supervised Methods | |||||||
| HARG-SSVM (Cho et al. ICCV 2013) | supervised | 0.584 | 0.552 | 0.912 | 0.444 | 0.666 | 0.632 |
| GMN (Zanfir et al. CVPR 2018) | supervised | 0.743 | 0.828 | 0.993 | 0.714 | 0.767 | 0.809 |
| PCA-GM (Wang et al. ICCV 2019) | supervised | 0.840 | 0.935 | 1.000 | 0.767 | 0.969 | 0.902 |
| DGMC (Fey et al. ICLR 2020) | supervised | 0.903 | 0.890 | 1.000 | 0.921 | 0.971 | 0.937 |
| CIE-H (Yu et al. ICLR 2020) | supervised | 0.822 | 0.812 | 1.000 | 0.900 | 0.976 | 0.902 |
| BBGM (Rolinek et al. ECCV 2020) | supervised | 0.968 | 0.899 | 1.000 | 0.998 | 0.994 | 0.972 |
| NMGM (Wang et al. PAMI 2021) | supervised | 0.973 | 0.854 | 1.000 | 0.860 | 0.977 | 0.933 |
| Unsupervised Methods | |||||||
| GANN (with HiPPI) | unsupervised | 0.845±0.313 | 0.868±0.1573 | 0.992±0.010 | 0.911±0.172 | 0.954±0.090 | 0.914 |
| GANN-GM (ours) | unsupervised | 0.854±0.261 | 0.898±0.226 | 1.000±0.000 | 0.886±0.186 | 0.964±0.104 | 0.920 |
| GANN-MGM~(ours) | unsupervised | 0.964±0.058 | 0.949±0.057 | 1.000±0.000 | 1.000±0.000 | 0.978±0.035 | 0.978 |
Experiment Results on Pascal VOC Keypoint dataset (2GM and MGM) (unfiltered setting): unsupervised pretraining + supervised finetuning is better than train from scratch.
| model | learning | backbone | #params | aero | bike | bird | boat | bottle | bus | car | cat | chair | cow | table | dog | horse | mbkie | person | plant | sheep | sofa | train | tv | mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GMN (Zanfir et al. CVPR 2018) | sup. | VGG16 | 12.9M | 28.0 | 55.0 | 33.1 | 27.0 | 79.1 | 52.2 | 26.0 | 40.2 | 28.4 | 36.0 | 29.8 | 33.7 | 39.4 | 43.0 | 22.1 | 71.8 | 30.8 | 25.9 | 58.8 | 78.0 | 41.9 |
| PCA-GM (Wang et al. ICCV 2019) | sup. | VGG16 | 41.7M | 27.5 | 56.5 | 36.6 | 27.7 | 77.8 | 49.2 | 23.9 | 42.3 | 27.4 | 38.2 | 38.7 | 36.5 | 39.3 | 42.8 | 25.6 | 74.3 | 32.6 | 24.7 | 51.5 | 74.3 | 42.4 |
| GANN-GM (ours) | unsup. | VGG16 | 12.4M | 12.6 | 19.5 | 16.6 | 18.5 | 41.1 | 32.4 | 19.3 | 12.3 | 24.3 | 17.2 | 38.0 | 12.2 | 15.9 | 18.2 | 19.4 | 35.5 | 14.8 | 15.4 | 41.5 | 60.8 | 24.3 |
| GANN-MGM (ours) | unsup. | VGG16 | 12.4M | 18.1 | 33.4 | 20.2 | 28.2 | 71.7 | 33.9 | 22.0 | 24.7 | 23.5 | 22.4 | 50.2 | 19.6 | 20.9 | 27.7 | 19.5 | 74.5 | 19.3 | 26.5 | 39.8 | 72.7 | 33.4 |
| ResNet34 | 21.3M | 16.4 | 37.4 | 23.2 | 29.5 | 80.8 | 33.6 | 24.1 | 17.8 | 26.9 | 22.6 | 53.4 | 16.9 | 21.8 | 30.1 | 23.3 | 86.0 | 19.7 | 31.7 | 39.0 | 71.5 | 35.3 | ||
| NGMv2 (Wang et al. PAMI 2021) | sup. | VGG16 | 71.4M | 45.9 | 66.6 | 57.2 | 47.3 | 87.4 | 64.8 | 50.5 | 59.9 | 39.7 | 60.9 | 42.1 | 58.3 | 58.5 | 61.9 | 44.6 | 94.5 | 50.1 | 35.2 | 73.1 | 82.1 | 59.0 |
| ResNet34 | 77.9M | 45.1 | 65.5 | 52.7 | 44.0 | 87.3 | 69.4 | 56.1 | 62.2 | 45.7 | 63.6 | 61.9 | 59.6 | 59.2 | 67.8 | 54.4 | 96.9 | 57.0 | 45.9 | 74.3 | 83.6 | 62.6 | ||
| BBGM (Rolinek et al. ECCV 2020) | sup. | VGG16 | 71.4M | 41.3 | 65.7 | 55.0 | 43.4 | 86.8 | 61.1 | 35.5 | 59.0 | 40.2 | 60.0 | 29.7 | 57.1 | 57.5 | 65.9 | 37.7 | 95.8 | 52.6 | 30.3 | 74.4 | 84.1 | 56.7 |
| ResNet34 | 77.9M | 38.1 | 69.1 | 54.2 | 45.0 | 87.0 | 74.7 | 43.3 | 62.3 | 48.3 | 63.7 | 63.8 | 60.9 | 60.4 | 65.4 | 50.2 | 97.1 | 56.2 | 45.9 | 78.4 | 82.2 | 62.3 | ||
| GANN-MGM (ours)+ NGMv2 (Wang et al. PAMI 2021) | unsup. | VGG16 | 71.4M | 47.0 | 69.4 | 53.7 | 46.3 | 85.7 | 67.6 | 59.0 | 60.2 | 45.9 | 61.0 | 29.9 | 57.9 | 59.5 | 63.2 | 47.4 | 92.2 | 51.5 | 39.9 | 71.6 | 78.3 | 59.4 (+0.4) |
| +sup. | ResNet34 | 77.9M | 46.5 | 66.2 | 56.5 | 46.5 | 85.9 | 73.8 | 57.4 | 61.4 | 47.3 | 65.7 | 63.9 | 59.4 | 60.1 | 70.6 | 54.7 | 94.3 | 57.0 | 51.8 | 74.9 | 82.4 | 63.8 (+1.2) | |
| GANN-MGM (ours) +BBGM (Rolinek et al. ECCV 2020) | unsup. | VGG16 | 71.4M | 43.0 | 69.2 | 55.3 | 46.3 | 85.4 | 66.7 | 53.3 | 61.4 | 46.7 | 64.0 | 33.7 | 61.7 | 60.7 | 64.0 | 43.9 | 94.0 | 54.9 | 52.3 | 78.0 | 80.0 | 60.7 (+4.0) |
| +sup. | ResNet34 | 77.9M | 39.6 | 68.9 | 56.2 | 46.7 | 87.4 | 71.9 | 44.5 | 62.0 | 47.9 | 65.8 | 50.8 | 62.6 | 61.6 | 62.9 | 49.4 | 96.9 | 59.6 | 49.7 | 80.6 | 85.3 | 62.5 (+0.2) |
Experiment Results on CUB2011 dataset (2GM and MGM): unsupervised models comparative to supervised models.
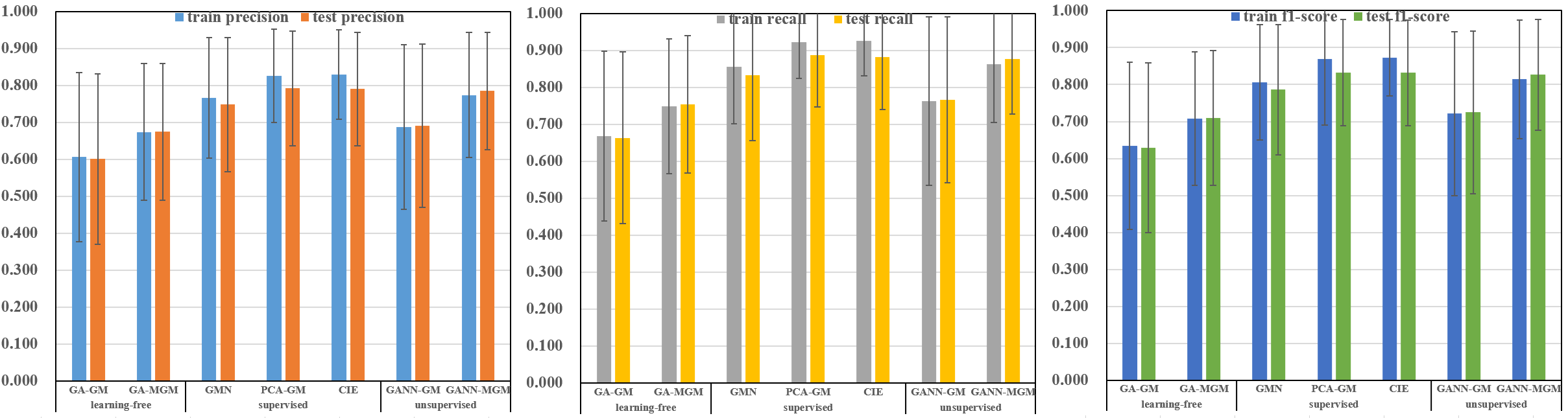
Figure 4. Mean and STD of precision, recall, and f1-score of graph matching with a single mode on CUB2011 dataset. MGM statics are computed from all graph pairs in each category, and two-graph matching statics are computed from 1000 random graph pairs. Improvement can be seen from our learning-free methods to our unsupervised methods, which are comparative with novel supervised learning methods on the testing set.
Experiment Results on Willow Object Class dataset (MGM3): unsupervised model better than learning-free algorithms.
| method | learning | 8 Cars, 8 Ducks, 8 Motorbikes | 40 Cars, 50 Ducks, 40 Motorbikes | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CP | RI | CA | MA | time (s) | CP | RI | CA | MA | time (s) | ||
| RRWM (Cho et al. ECCV 2010) | free | 0.879 | 0.871 | 0.815 | 0.748 | 0.4 | 0.962 | 0.949 | 0.926 | 0.751 | 8.8 |
| CAO-C (Yan et al. PAMI 2016) | free | 0.908 | 0.903 | 0.86 | 0.878 | 3.3 | 0.971 | 0.96 | 0.956 | 0.906 | 1051.5 |
| CAO-PC (Yan et al. PAMI 2016) | free | 0.887 | 0.883 | 0.831 | 0.87 | 1.8 | 0.971 | 0.96 | 0.956 | 0.886 | 184.0 |
| DPMC (Wang et al. AAAI 2020) | free | 0.931 | 0.923 | 0.89 | 0.872 | 1.2 | 0.969 | 0.959 | 0.948 | 0.941 | 97.5 |
| GA-MGM3 (ours) | free | 0.921 | 0.905 | 0.893 | 0.653 | 10.6 | 0.89 | 0.871 | 0.85 | 0.669 | 107.8 |
| GANN-MGM3 (ours) | unsupervised | 0.976 | 0.970 | 0.963 | 0.896 | 5.2 | 0.974 | 0.968 | 0.956 | 0.906 | 80.7 |
Experiment Results on CUB2011 and Pascal VOC Keypoint dataset (MGM3)
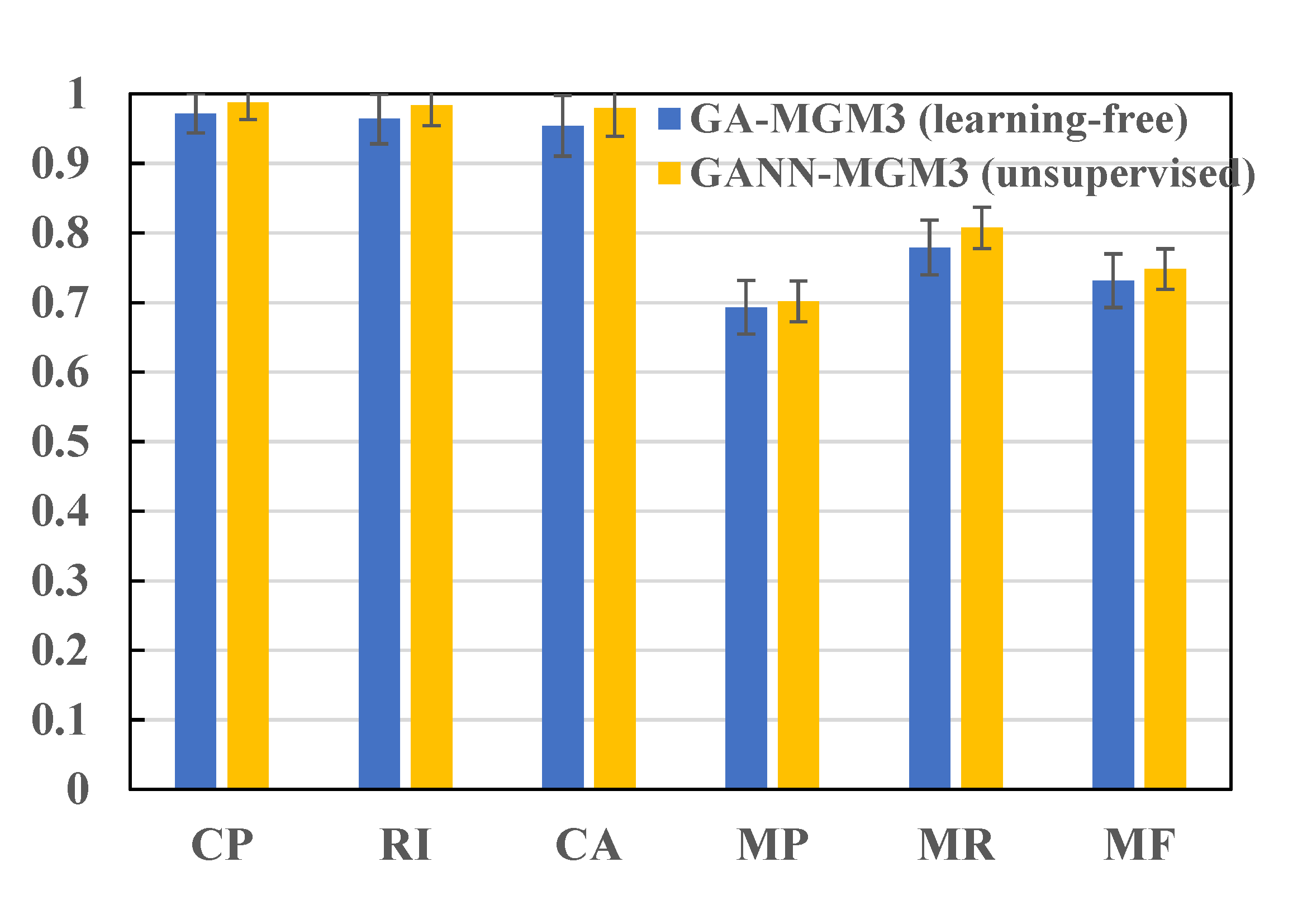
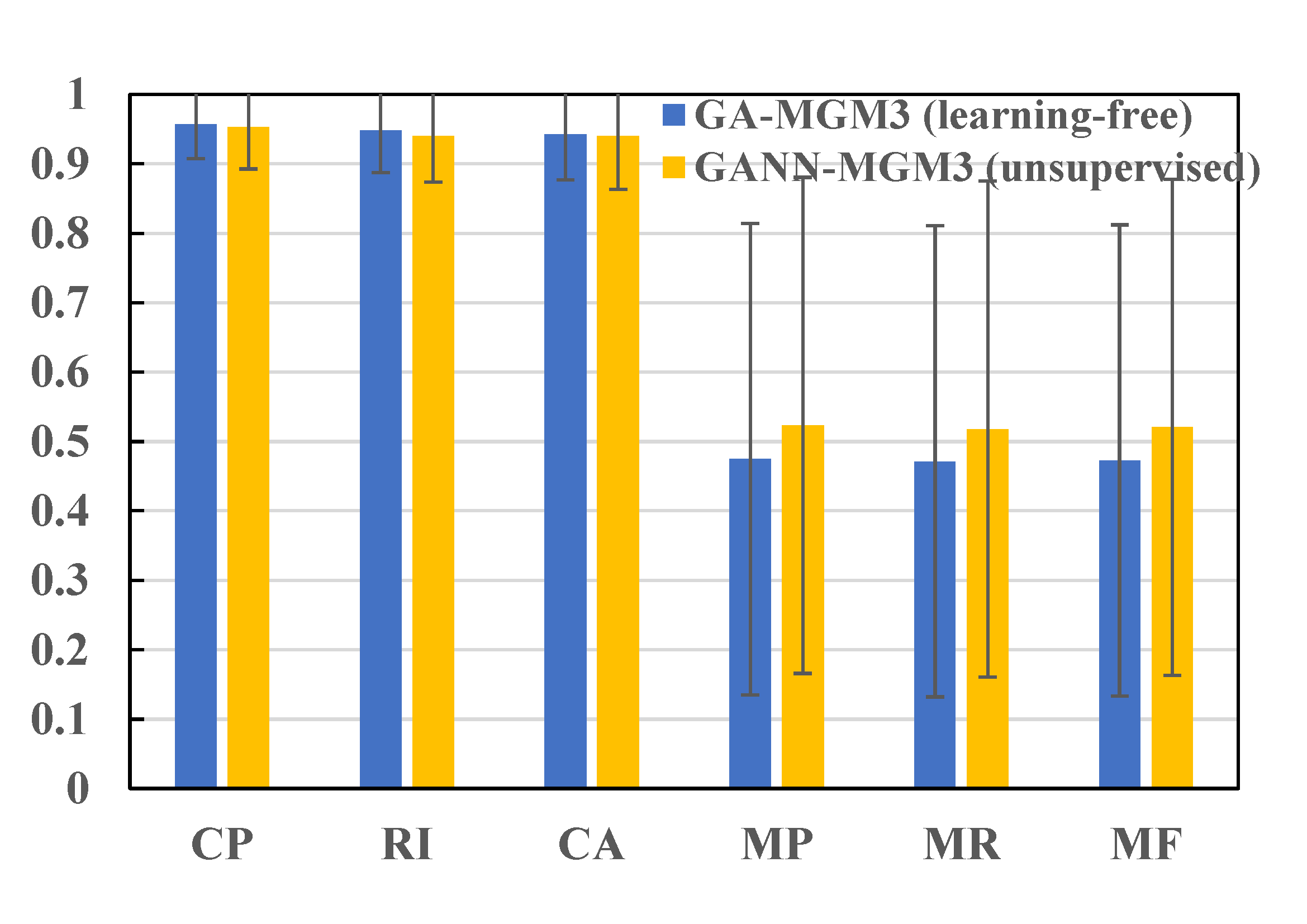
Figure 5&6. Experiment result on Pascal VOC Keypoint dataset for initializing VGG16 weights of NGMv2 and BBGM by the proposed unsupervised learning model GANN-MGM3. Without modifying any model architectures, the unsupervised pretraining by GANN-MGM3 leads to faster convergence and better performance compared to the versions initialized by ImageNet classification weights.